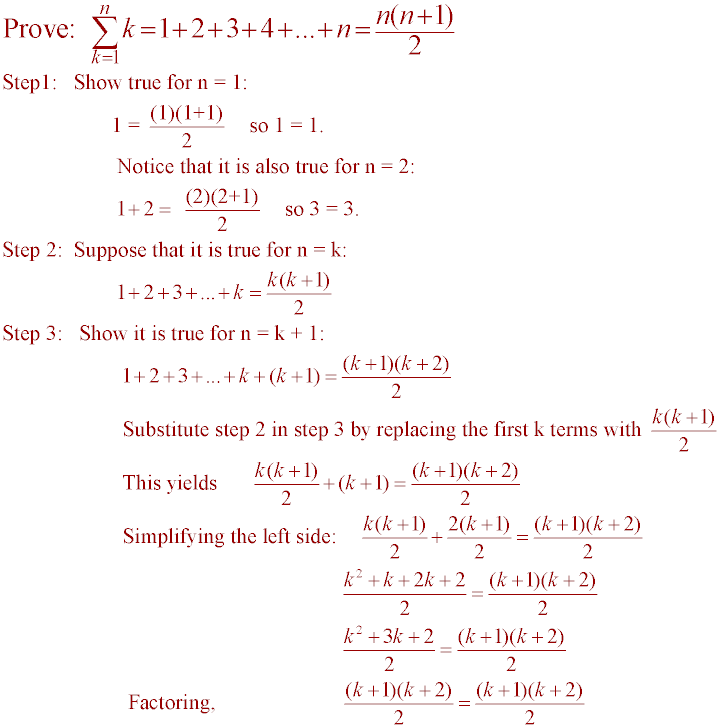Mathematical Induction Word Problems With Solutions
University of Western Australia DEPARTMENT OF MATHEMATICS UWA ACADEMY FOR YOUNG MATHEMATICIANS Induction. 4 By the principle of mathematical induction prove that for n 1.

Mathematical Induction Part 2 Nicole Ling Brilliant
4n 1 n2n 1 a Check the basis step.
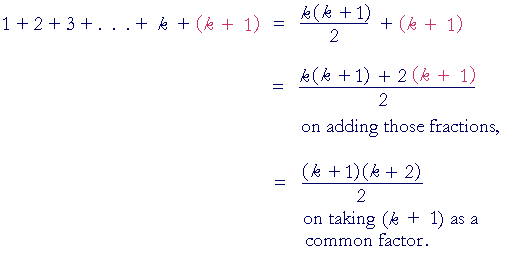
Mathematical induction word problems with solutions. Learn how to use Mathematical Induction in this free math video tutorial by Marios Math Tutoring. Xk1 p 12xk 124 p 9 3 4. Recall from secondary school the definition n k n.
Dont use ghetto Pn lingo. Practice the mathematical induction questions given below for the better understanding of the concept. Mathematics intermediate first year 1A and 1B solutions for some problems.
So it is true. Suppose you start by splitting such that y is empty and z R. After having gone through the stuff given above we hope that the students would have understood Mathematical Induction Problems With Solutions.
And the recursion relation n k n1 k 1 n1 k For appropriate values of n and k. It remains to show that Pk1 holds that is that xk1 4. P1 is true.
Let us assume that the statement is true for n k. 4 n 1 n 2 n 1 3 7 11. Write Base Case and prove the base case holds for na.
Since LHS RHS. 1 for every n 0. 3 Prove that the sum of the first n non-zero even numbers is n2 n.
Finally here are some identities involving the binomial coefficients which can be proved by induction. So LHS 1 3 5 9. The solution in mathematical induction consists of the following steps.
1 For Pk 1 The bottom series is arithmetic by 1 Pk 1 is true. Functions mathematical induction functions addition of vectors trigonometric ratios upto transformations trigonometric equations hyperbolic. Hence p 2 is true.
Sum _ r1 n 2r-1quad quad n 2 quad forquad allquad nin Z r1n. Let y 0 track the number of 0 s in y currently 0 and z 1 the number of 1s in z starts at some number I 0. N 1 n n 1 n 23.
RHS 3 2 9. Example if we are to prove that 1234. 1 3 2 3 3 3 n 3 n n 12 2.
Nnn12 we say let Pn be 1234. Write Induction Hypothesis say Assume ___ for some 𝑘𝑎. Hence 1 3 2n-1 n 2 for n 3.
Math Word Problems Questions and Answers. If the currently leftmost digit in z is a 0 y 0 increases by 1. The first principle of Mathematical Induction points that when a base step and the inductive step are established as true it can be concluded that the initial statement Pn is true for all natural numbers.
MATHEMATICAL INDUCTION INTERMEDIATE FIRST YEAR PROBLEMS WITH SOLUTIONS. Put n 2. It is a useful exercise to prove the recursion relation you dont need induction.
Show that 0123n nn1 2. 12 23 34 n. Mathematical Induction Tom Davis 1 Knocking Down Dominoes The natural numbers N is the set of all non-negative integers.
We know that T k k k12 the assumption above T k1 has an extra row of k 1 dots. Else its a 1 and z 1 decreases by one. Let p n 1 1 2 1 1 2 3 1 1 2 3 4 1 1 2 3 n n 1 n 1 Step 1.
Left 4n - 1 right nleft 2n 1 right 3 7 11. State the claim you are proving. Quite often we wish to prove some mathematical statement about every member of N.
2n 1 2 x 3 1 6 -1 5. Write the statement to be proved as Pn where n is the variable in the statement and P is the statement itself. Fix k 1 and suppose that Pk holds that is xk 4.
1 2 3 2 5 2 2n 1 2 n 2n 1 2n 13. The statement P1 says that x1 1 4 which is true. These solutions are very simple to understand.
N1 n 1 if it is true. Get help with your Math Word Problems homework. You can find ample problems based on this principle and their solutions in Mathematical Induction Class 11 NCERT Solutions.
Apart from the stuff given above if you want to know more about Mathematical Induction Problems With Solutions. Problems for Principle of Mathematical Induction. Problems with Solutions Greg Gamble 1.
R 1 n 2 r 1 n 2 f o r a l l n Z. We go through two examples in this video030 Explanation. For any n 1 let Pn be the statement that xn 4.
Use the mathematical to prove that the formula is true for all natural numbers. Thus by the principle of mathematical induction for all n 1 Pn holds. Access the answers to hundreds of Math Word Problems questions that are.
K 1 k 2 k k 1 2 k 1 k 1 k 2 k 2 k 1 They are the same. P 2 p n 1 1 2 2 1 2 1 13 13. Using the Principle of Mathematical Induction prove that.
Junior inter 1A. Assume that Pk is true for some natural number k that is. As a very simple example consider the following problem.
By the Principle of Mathematical Induction Pn is true for all natural numbers n. 3 7 1 1. So T k1 T k k 1 k1 k22 k k1 2 k1 Multiply all terms by 2.
Now repeatedly shift the division one to the right. Let Pn be the proposition. Mathematical Induction Examples Worksheet The Method.

Principle Of Mathematical Induction Introduction Videos And Examples

Proof By Induction Steps Examples Study Com

Proof By Induction W 9 Step By Step Examples
An Example Of A Proof By Mathematical Induction
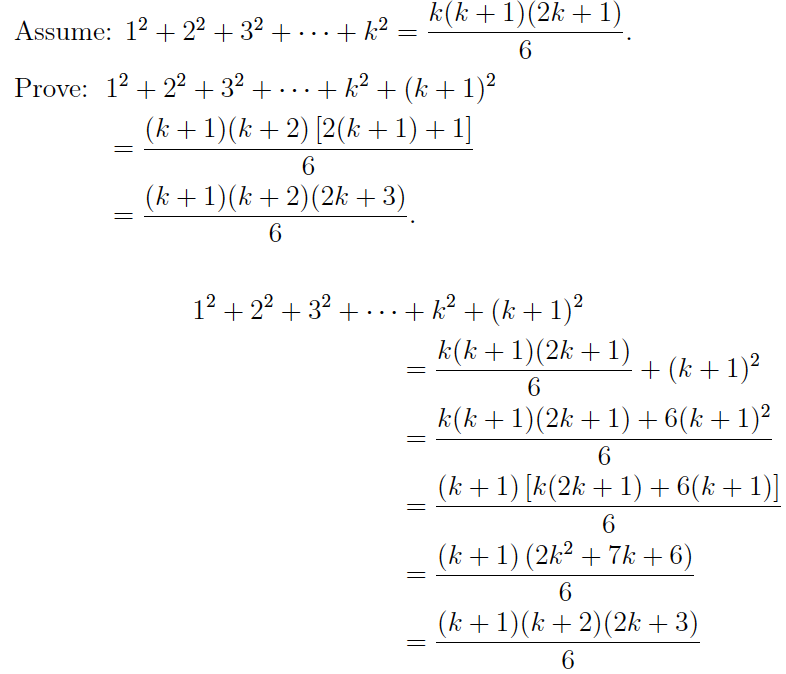
Principle Of Mathematical Induction Study Material For Iit Jee Askiitians

Mathematical Induction With Videos Worksheets Games Activities

Mathematical Induction Examples Solutions Youtube

Examples Of Mathematical Induction Examples Videos Worksheets Solutions Activities
Proof Mathematical Induction Payment Proof 2020

Mathematical Induction Practice Problems Youtube
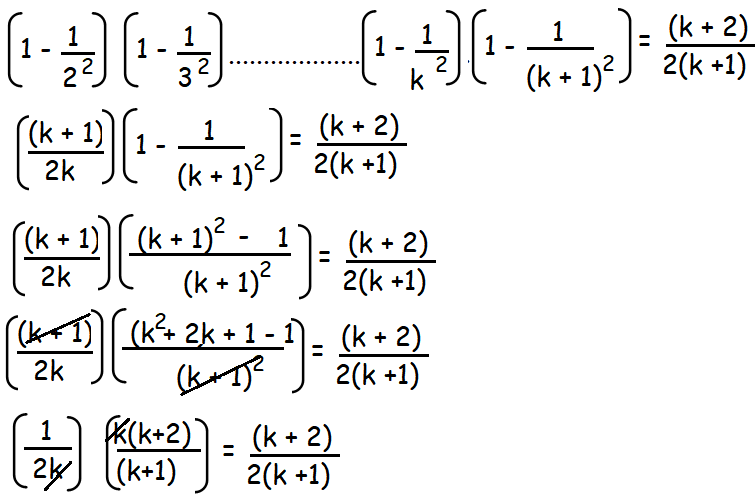
Principle Of Mathematical Induction Examples

Proof Writing How To Write A Clear Induction Proof Mathematics Stack Exchange

Proof By Mathematical Induction

Proof By Induction W 9 Step By Step Examples

Mathematical Induction Tutorial

Have Spent A Long Time On A Proof By Induction Topic With 29 Fully Worked Solutions Http Adaprojec Mathematical Induction Discrete Mathematics Number Theory

Using Proof By Mathematical Induction Example On Chegg Com
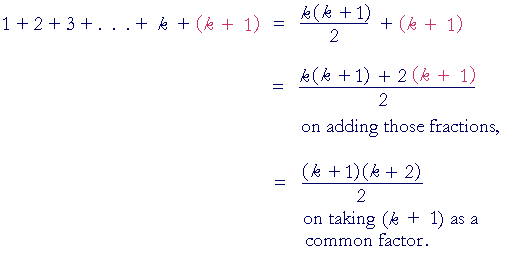
Mathematical Induction Topics In Precalculus